ある四辺形領域
![]() 、
、
![]() における
関数
における
関数 ![]() について、
について、
| (3.9) |
その積分は、
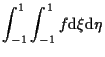 |
|||
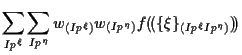 |
(3.10) |
ここで、
![]() は、
各次元方向の積分点
は、
各次元方向の積分点
![]() の自然座標であり、
の自然座標であり、
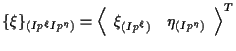 |
(3.11) |
![]() は一次元線分の
は一次元線分の ![]() 座標における積分点座標、
座標における積分点座標、
![]() は一次元線分の
は一次元線分の ![]() 座標における積分点座標である。
座標における積分点座標である。
また、
![]() は、
各次元方向の積分点
は、
各次元方向の積分点
![]() の重み係数である。
の重み係数である。
各方向の数値積分の座標と重みについては、 前節の「一次元」を参照。
なお、 四辺形の境界稜線上の関数の積分は、 一次元線分上のガウス積分を用いればよい。 前節の「一次元」を参照。