| (1.1) |
(参考文献:Numerical Recipes in C, 5.5 二次方程式、三次方程式)
二次方程式は以下のように定義される。
| (1.1) |
ここで、
![]() は求めるべき解であり、
は求めるべき解であり、
![]() は非ゼロのスカラー、
は非ゼロのスカラー、
![]() 、
、![]() はスカラーである。
はスカラーである。
この方程式の解 ![]() の種類は、
以下の判別式
の種類は、
以下の判別式 ![]() によって決定される。
によって決定される。
| (1.2) |
もし、![]() が0の場合、解は一つの重根
が0の場合、解は一つの重根 ![]() となる。
となる。
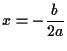 |
(1.3) |
もし、![]() が正の場合、解は二つの実根
が正の場合、解は二つの実根 ![]() 、
、![]() となる。
となる。
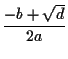 |
|||
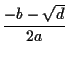 |
(1.4) |
もし、![]() が負の場合、解は二つの虚根となる。
が負の場合、解は二つの虚根となる。
なお、解をロバストに求めるために、以下の手法を用いる。
まず、以下の ![]() を求める。
を求める。
| (1.5) |
これを用いて、
| (1.6) |