オブジェクト指向並列行列ソルバークラス

-- FMM3Dにおける行列ソルバークラス --


Contents
  1. 行列ソルバーとは？

  2. 従来の行列ソルバ

  3. オブジェクト指向型行列ソルバークラス

  4. 行列ソルバークラスによる行列計算法

  5. 並列版の行列ソルバーとクラス

行列ソルバーとは

行列ソルバーとは、以下の行列方程式の解xを求めるためのプログラムである。

K x = F

ここで、K は行列で、x と F はベクトルである。
FEMの世界では、K を剛性行列、 F を加重項ベクトルと呼ぶ事が多い。

従来の行列ソルバー
  1. 従来の行列ソルバーは、 多くの引数を伴ったサ１つのブルーチンで実現されていた。

  2. そのため、行列ソルバーを使うためには、 引数である行列を作成する必要がある。

  3. しかし、通常の反復法の行列ソルバーに用いられる行列は、
    単なる2次元配列ではなく、メモリの節約から非ゼロ成分だけを持つ事が多い。

  4. つまり、行列の各成分の値と、行列のどの成分かの組を持つ事になる。
    しかも、対角成分、上三角、下三角行列に別けて持つ事が多い。

このようなデータを利用者に作成させる行列ソルバーは、 非常に使いにくいものである。

オブジェクト指向の行列ソルバー
  1. データをクラス内部に隠蔽するため 利用者はデータ構造を知る必要が無い
    (利用者はマトリックスを構成する配列データや袖領域データを作成しない)

  2. 配列などは、サイズ指定する時に動的に作成される

  3. 幾つかのメソッドを利用するだけで、行列計算が可能

  4. メソッドの引数はすべてスカラ (引数に配列は無い)

  5. 行列ソルバーを利用するプログラマが ソースを読まなくとも利用可能

  6. 以下のようなメソッド群を利用するだけで行列計算が行える


    7. 関数名 機能
    minit(n,f) 行列の初期化とメモリ確保 n:節点数、f:各節点の自由度
    mclear() 剛性行列 K と加重項ベクトル F のゼロクリア
    maxc(n) 最大反復回数を n に設定する（デフォルト値は 1000）
    resd(R) 収束判定誤差を R に設定する（デフォルト値は 1.0d-8）
    setk(i,j,R) 剛性行列Kのi,j要素の値をRに設定する
    addk(i,j,R) 剛性行列Kのi,j要素の値にRを足す(setkとaddkでKマトリクスを作成する)
    setf(i,R) 加重項ベクトルFのi要素の値をRに設定する
    addf(i,R) 加重項ベクトルi要素の値にRを足す(setfとaddfでFベクトルを作成する)
    dirc(i,R) ディレクレ条件を設定する(K マトリクスと F ベクトルを修正)
    mcheck() 剛性行列 K の対角優位性をチェックし、対角優位で無い行の行数を返す
    msolve() CG法ソルバー：行列を解き、解ベクトル X を求める。収束時には0を返す
    geta(i) i番目の解を参照する
    getk(i,j) 剛性行列のi,j要素の値を参照する(デバッグ用)
    getf(i) i番目の加重項ベクトルの値を参照する(デバッグ用)
    mdelete() 全メモリを開放(プログラムの最後に実行する)

    Methods in CG Solver class
行列ソルバークラスによる行列計算法

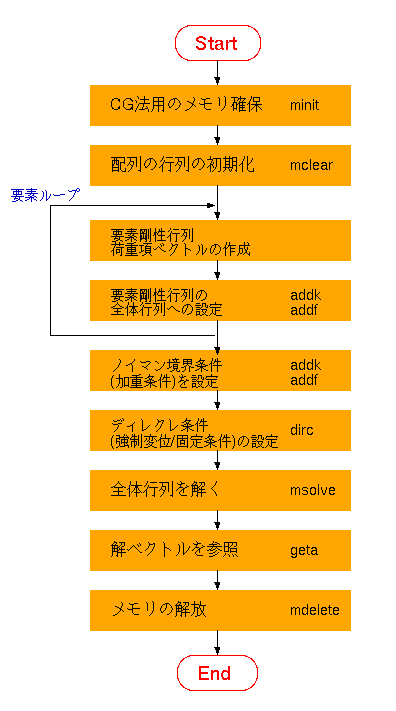
計算手順 解析手順例(FEMによる解析)
  1. minit(n,f)関数を使って、行列の大きさを設定しメモリ確保を行う。 (行列の大きさNは節点数×各節点の自由度となる)

  2. mclear()で剛性行列Kと加重項ベクトルFを零クリアする。

  3. 剛性行列 K の各i,j成分を setk(i,j,R)及びaddk(i,j,R)を用いて設定する。 (剛性行列のデータフォーマットを考える必要は無い)

  4. 加重項ベクトルFを setf(i,R)及びaddf(i,R)を用いて設定する。

  5. ノイマン境界条件がある場合にはaddk(i,j,R)及びaddf(i,R)を用いて設定する。

  6. ディレクレ条件がある場合にはdirc(i,R)を用いて設定する。

  7. msolve()関数を用いて、解xを計算する。 (引数は何も無い)

  8. geta(i)やgeta(i,f)関数を用いて解を参照する。 ( a = get(i) で i番目の解を取得)

  9. 必要無くなったら mdelete() でメモリを解放できる



並列版の行列ソルバークラス
  1. 単CPU用クラスを並列用クラスが継承
  2. 袖領域の情報は内部で自動作成→通信関連データの入力は無し
  3. グローバルな節点番号と担当PE番号を指定する関数が増えるだけ
  4. 並列行列ソルバーの利用者はMPIの事は一切考える必要がない
単CPU用 並列版 機能
minit(N,F) minit(N,F,Na) Initialize (N:num.of nodes, F:deg.of freedum)
mclear() mclear() zero clear of K and f.
maxc(N) ← Set number of Iteration to N.
resd(R) ← Set Residual to R.
setk(i,j,R)← Set i,j-element of K to R.
setf(i,R) ← Set i-th element of f to R.
addk(i,j,R)← Add R to i,j-element of K.
addf(i,R) ← Add R to i-th element of f
msolve() msolve() solve and calculate x.
geta(i) ← get i-th element of x
- setnd(n,i) Set global node number to i.
- setpe(n,i) Set PE number to i.

行列ソルバークラスのメソッド一覧