解説

現配置 $t$ における平衡方程式は、

$$\frac{ \partial {}^{t} [ \sigma ] }{ \partial {}^{t} \{ x \} } + {}^{t} \{ b \} = {}^{t} \rho {}^{t} \{ a \}$$ (7.28)

ここで、 ${}^{t} [ \sigma ]$ はCauchy応力、 ${}^{t} \{ b \}$ は単位体積当りの体積力、 ${}^{t} \rho$ は質量密度、 ${}^{t} \{ a \}$ は加速度である。

なお、静的問題では、

$$\frac{ \partial {}^{t} [ \sigma ] }{ \partial {}^{t} \{ x \} } + {}^{t} \{ b \} = 0$$ (7.29)

一方、 基準配置 $t = o$ における平衡方程式は、

$$\frac{ \partial {}_{o}^{t} [ \Pi ] }{ \partial \{ X \} } + {}_{o}^{t} \{ \tilde{b} \} = {}^{o} \rho {}^{t} \{ a \}$$ (7.30)

ここで、 ${}_{o}^{t} [ \Pi ]$ は第１Piola-Kirchhoff応力であり、 これは、

$${}_{o}^{t} [ \Pi ] = {}_{o}^{t} [ S ] \cdot { {}_{o}^{t} [ F ] } ^ { T }$$ (7.31)

ここで、 ${}_{o}^{t} [ S ]$ は第２Piola-Kirchhoff応力、 ${}_{o}^{t} [ F ]$ は変形勾配である。

${}_{o}^{t} \{ \tilde{b} \}$ は 時刻 $t = o$ を基準とした単位体積当りの体積力であり、

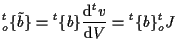$${}_{o}^{t} \{ \tilde{b} \} = {}^{t} \{ b \} \frac{ \mathrm{d} {}^{t} v }{ \mathrm{d} V } = {}^{t} \{ b \} {}_{o}^{t} J$$ (7.32)

なお、静的問題では、

$$\frac{ \partial {}_{o}^{t} [ \Pi ] }{ \partial \{ X \} } + {}^{t} \{ b \} = 0$$ (7.33)