表面上の法線方向成分指定の積分

要素 $Ie$ 境界表面 $Iface$ において、 ${}^{t} f$ を、 あるベクトル量の法線方向成分を表すスカラー関数であるとする。

$${}^{t} f = f ( \! ( \{ \xi \} ) \! )$$ (5.75)

このベクトルの積分は、 $\xi = \pm 1, \eta = \pm 1, \zeta = \pm 1$ の表面についてそれぞれ 以下のように定義される。

$\xi = \pm 1$ の表面の場合、

$$\int_{S_{(Iface)}} {}^{t} f \{ n \} \mathrm{d} S$$

$$= \int_{-1}^1 \int_{-1}^1 {}^{t} f \{ J^S \} \mathrm{d} \eta \mathrm{d} \zeta$$

$$= \sum_{Ip} w_{(Ip)} f ( \! ( \{ \xi \} _{(Ip)} ) \! ) \{ J^S \} ( \! ( \{ \xi \} _{(Ip)} ) \! )$$

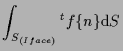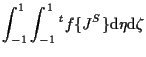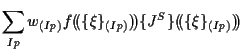ここで、 表面積分の変換子 $\{ J^S \}$ は、

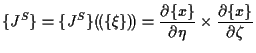$$\{ J^S \} = \{ J^S \} ( \! ( \{ \xi \} ) \! ) = \frac{ \partial \{ x \} }{ \partial \eta } \times \frac{ \partial \{ x \} }{ \partial \zeta }$$ (5.76)

各方向の数値積分の座標と重みについては、 前パラグラフの「境界積分」を参照。

$\eta = \pm 1$ の表面の場合、

$$\int_{S_{(Iface)}} {}^{t} f \{ n \} \mathrm{d} S$$

$$= \int_{-1}^1 \int_{-1}^1 {}^{t} f \{ J^S \} \mathrm{d} \zeta \mathrm{d} \xi$$

$$= \sum_{Ip} w_{(Ip)} f ( \! ( \{ \xi \} _{(Ip)} ) \! ) \{ J^S \} ( \! ( \{ \xi \} _{(Ip)} ) \! )$$

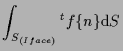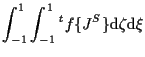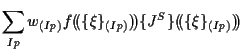ここで、 表面積分の変換子 $\{ J^S \}$ は、

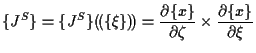$$\{ J^S \} = \{ J^S \} ( \! ( \{ \xi \} ) \! ) = \frac{ \partial \{ x \} }{ \partial \zeta } \times \frac{ \partial \{ x \} }{ \partial \xi }$$ (5.77)

各方向の数値積分の座標と重みについては、 前パラグラフの「境界積分」を参照。

$\zeta = \pm 1$ の表面の場合、

$$\int_{S_{(Iface)}} {}^{t} f \{ n \} \mathrm{d} S$$

$$= \int_{-1}^1 \int_{-1}^1 {}^{t} f \{ J^S \} \mathrm{d} \xi \mathrm{d} \eta$$

$$= \sum_{Ip} w_{(Ip)} f ( \! ( \{ \xi \} _{(Ip)} ) \! ) \{ J^S \} ( \! ( \{ \xi \} _{(Ip)} ) \! )$$

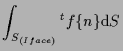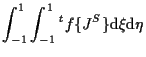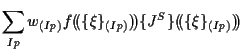ここで、 表面積分の変換子 $\{ J^S \}$ は、

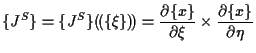$$\{ J^S \} = \{ J^S \} ( \! ( \{ \xi \} ) \! ) = \frac{ \partial \{ x \} }{ \partial \xi } \times \frac{ \partial \{ x \} }{ \partial \eta }$$ (5.78)

各方向の数値積分の座標と重みについては、 前パラグラフの「境界積分」を参照。