解説

重み関数を $T^*$ とする。 ただし、ディリクレ境界条件が指定された境界 $S = S^T$ 上において $T^* = 0$ とする。

まず、 熱伝導方程式、および、熱流束境界条件式の残差をとり、 これに重み関数を乗じて積分することにより、 以下のように重みつき残差表示式が成り立つ。

$$\int_V T^* ( - \mathrm{div} {}^{t} \{ q \} + {}^{t} q^{body} - \rho c {}^{t} \dot{T} ) \mathrm{d} V$$

$$+ \int_{S^q} T^* ( {}^{t} \{ q \} \cdot \{ n \} - {}^{t} q ) \mathrm{d} S$$

$$= 0$$ (1.14)

これを展開すると、

$$- \int_V T^* \mathrm{div} {}^{t} \{ q \} \mathrm{d} V + \int_V T^* {}^{t} q^{body} \mathrm{d} V - \int_V T^* \rho c {}^{t} \dot{T} \mathrm{d} V$$

$$+ \int_{S^q} T^* {}^{t} \{ q \} \cdot \{ n \} \mathrm{d} S - \int_{S^q} T^* {}^{t} q \mathrm{d} S$$

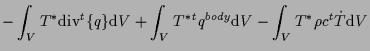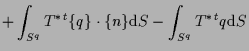$$= 0$$ (1.15)

一方、発散定理により、

$$\int_V T^* \mathrm{div} {}^{t} \{ q \} \mathrm{d} V$$

$$= \int_{S} T^* {}^{t} \{ q \} \cdot \{ n \} \mathrm{d} S - \int_V \frac{ \partial T^* }{ \partial \{ x \} } \cdot {}^{t} \{ q \} \mathrm{d} V$$

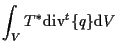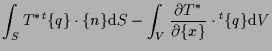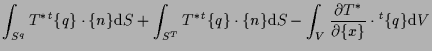$$= \int_{S^q} T^* {}^{t} \{ q \} \cdot \{ n \} \mathrm{d} S + \int_{... ...t_V \frac{ \partial T^* }{ \partial \{ x \} } \cdot {}^{t} \{ q \} \mathrm{d} V$$ (1.16)

このうち、 温度境界 $S = S^T$ 上における重み関数 $T^* = 0$ の条件から、 右辺第2項はゼロとなる。

さらに、 熱流束境界 $S = S^{direct}$ 、 熱伝達境界 $S = S^{cnv}$ から、 最終的に重みつき残差式の弱形式が以下のように導かれる。

$$\int_V \frac{ \partial T^* }{ \partial \{ x \} } \cdot ( [ \lambd... ...v}} T^* h {}^{t} T \mathrm{d} S + \int_V T^* \rho c {}^{t} \dot{T} \mathrm{d} V$$

$$= \int_V T^* {}^{t} q^{body} \mathrm{d} V - \int_{S^{direct}} T^* {}^{t} q^{direct} \mathrm{d} S + \int_{S^{cnv}} T^* h {}^{t} T^{env} \mathrm{d} S$$

アインシュタイン標記では、

$$\int_V \frac{ \partial T^* }{ \partial x_i } \lambda_{ij} \frac{ ... ...v}} T^* h {}^{t} T \mathrm{d} S + \int_V T^* \rho c {}^{t} \dot{T} \mathrm{d} V$$

$$= \int_V T^* {}^{t} q^{body} \mathrm{d} V - \int_{S^{direct}} T^* {}^{t} q^{direct} \mathrm{d} S + \int_{S^{cnv}} T^* h {}^{t} T^{env} \mathrm{d} S$$

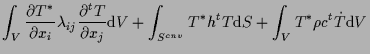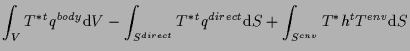ここで、 左辺第1項は熱伝導項、 左辺第2項は熱伝達項、 左辺第3項は熱容量項、 右辺第1項は内部発熱項、 右辺第2項は熱流束項、 右辺第3項は熱伝達項である。