形状関数の体積座標 ![]() に関する微分
に関する微分
![]() は、
は、
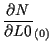 |
|||
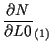 |
|||
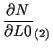 |
|||
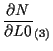 |
(3.32) |
体積座標 ![]() に関する微分
に関する微分
![]() については、
については、
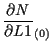 |
|||
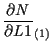 |
|||
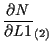 |
|||
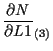 |
(3.33) |
体積座標 ![]() に関する微分
に関する微分
![]() については、
については、
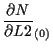 |
|||
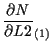 |
|||
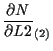 |
|||
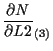 |
(3.34) |
体積座標 ![]() に関する微分
に関する微分
![]() については、
については、
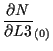 |
|||
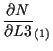 |
|||
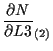 |
|||
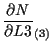 |
(3.35) |
したがって、
形状関数の自然座標 ![]() に関する
微分
に関する
微分
![]() は、
式
3.25
より、
は、
式
3.25
より、
| (3.36) |
| (3.37) |
| (3.38) |