位置 ${}^{t} \{ x \}$

２次元アイソパラメトリック要素では、 位置 ${}^{t} \{ x \}$ は２次元ベクトルである。

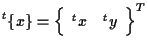$${}^{t} \{ x \} = { \left\{ \begin{array}{cc} {}^{t} x & {}^{t} y \end{array} \right\} } ^ { T }$$ (5.4)

位置は自然座標 $\{ \xi \}$ の関数であり、 節点位置座標 ${}^{t} \{ x \} _{(In)}$ や その他の付加情報を用いて補間される。

$${}^{t} \{ x \} = \{ x \} ( \! ( \{ \xi \} ) \! )$$ (5.5)

なお、 構造解析でのフレーム要素などでは、 節点位置座標に加えて、 法線方向などの情報が用いられる。

Euler型またはLagrange型の微小変形問題では、 これは時間に依存しない。 Lagrange型の有限変形問題の場合、 このベクトルは時間または増分とともに変化する。 すなわち、 Euler型またはLagrange型の微小変形問題では、これらは解析形状情報であり、 一方、 有限変形問題では、これらは初期値だけを与えられる未知数となる。

Lagrange型の有限変形問題では、位置、微分および積分について、 初期位置 $\{ X \}$ か 現在位置 ${}^{t} \{ x \}$ に関するものの区別が必要となる。

以後の説明では、 現在位置 ${}^{t} \{ x \}$ に関する位置、微分、積分についてだけ記述し、 初期位置については、 節点の位置や局所座標軸ベクトルなどを初期配置に直して評価することとする。