物体に作用する力として、
単位体積当りの物体力 body force ベクトル
![]() と、
単位面積当りの表面力 surface force ベクトル
と、
単位面積当りの表面力 surface force ベクトル
![]() とがある。
とがある。
また、運動量 momentum は
![]() であるから、
Eulerの第1運動法則 Euler's first law of motion は、
であるから、
Eulerの第1運動法則 Euler's first law of motion は、
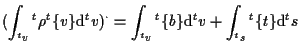 |
(6.89) |
これは、
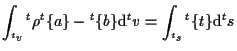 |
(6.90) |
ここで、
![]() は
物質点の加速度ベクトルである。
は
物質点の加速度ベクトルである。
角運動量 angular momentumの保存について、 Eulerの第2運動法則 Euler's second law of motion は、
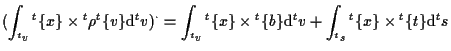 |
(6.91) |
これは、
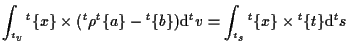 |
(6.92) |