![$\displaystyle \int_V
{}^{t} [ \sigma ] : \delta {}^{t} [ \epsilon ]
\mathrm{d} V$](img1071.png) |
|||
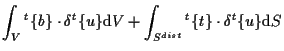 |
|||
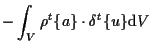 |
(7.11) |
微小変形の線形弾性問題での 仮想仕事の原理式 principle of virtual work は、
![$\displaystyle \int_V
{}^{t} [ \sigma ] : \delta {}^{t} [ \epsilon ]
\mathrm{d} V$](img1071.png) |
|||
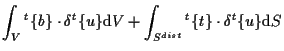 |
|||
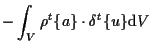 |
(7.11) |
ここで、
![]() は仮想変位、
は仮想変位、
![]() は仮想歪み
である。
は仮想歪み
である。
この仮想仕事項に、応力歪み式 7.1 を代入すると、
なお、ここで用いられている変数としては、
材料定数 ![]() 、
、![]() および、
荷重
および、
荷重
![]() 、
、
![]() 、
、
![]() 、
、
![]() は既知であり、
は既知であり、
![]() 、
、
![]() は未知であり、
一方、
は未知であり、
一方、
![]() は任意の値をとり、
は任意の値をとり、
![]() は
は
![]() より導出される。
より導出される。
また、静的問題の場合には、 慣性力項を無視することにより、
この場合、未知数は
![]() だけになる。
だけになる。