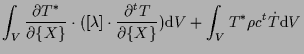 |
|||
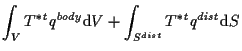 |
|||
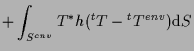 |
(12.16) |
線形の熱伝導問題の重みつき残差表現は、 (式 10.8 参照)
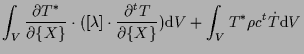 |
|||
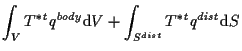 |
|||
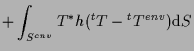 |
(12.16) |
ここで、 左辺第1項は熱伝導項、 左辺第2項は熱容量項、 右辺第1項は内部発熱項、 右辺第2項は熱流束項(分布熱流束、および集中熱流束)、 右辺第3項は熱伝達項である。
これに上記の未知数の有限要素補間式を代入すると、 (各項については、以下の各節で具体例に説明する。)
| (12.17) |
ここで、
要素 ![]() について、
について、
![]() は
要素熱伝導行列
は
要素熱伝導行列
![]() の
節点
の
節点 ![]() 節点
節点 ![]() に関する成分である。
に関する成分である。
![]() は
要素熱容量行列
は
要素熱容量行列
![]() の
節点
の
節点 ![]() 節点
節点 ![]() に関する成分である。
に関する成分である。
![]() は
要素内部発熱項ベクトル
は
要素内部発熱項ベクトル
![]() の
節点
の
節点 ![]() に関する成分である。
に関する成分である。
要素 ![]() の境界
の境界 ![]() について、
について、
![]() は
要素熱伝達行列
は
要素熱伝達行列
![]() の
節点
の
節点 ![]() 節点
節点 ![]() に関する成分である。
に関する成分である。
![]() は
要素分布熱流束項ベクトル
は
要素分布熱流束項ベクトル
![]() の
節点
の
節点 ![]() に関する成分である。
に関する成分である。
![]() は
要素熱伝達項ベクトル
は
要素熱伝達項ベクトル
![]() の
節点
の
節点 ![]() に関する成分である。
に関する成分である。
節点 ![]() について、
について、
![]() は
全体集中熱流束項ベクトル
は
全体集中熱流束項ベクトル
![]() の
節点
の
節点 ![]() に関する成分である。
に関する成分である。
この式は、任意の温度の重み関数 ![]() について
成り立たねばならないから、すべての自由度
について
成り立たねばならないから、すべての自由度 ![]() について、
について、
| (12.18) |
すなわち、
| (12.19) |
ここで、
![]() 、
、
![]() はそれぞれ、
システム全体での温度とその変化速度の列ベクトルである。
はそれぞれ、
システム全体での温度とその変化速度の列ベクトルである。
そして、最終的に上記の有限要素離散化式が得られる。