要素 ![]() 境界稜線
境界稜線 ![]() において、
関数
において、
関数 ![]() を、
長さ当たりの量を表すものとする。
を、
長さ当たりの量を表すものとする。
| (1.27) |
その稜線上での境界積分は、以下のように表される。
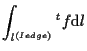 |
(1.28) |
この具体的な表現は、各要素タイプによってそれぞれ定義される。
もし、
関数 ![]() が面積座標
が面積座標 ![]() の多項式で表現されるならば、
その稜線上での境界積分は、
以下の面積座標公式によって求めることが出来る。
の多項式で表現されるならば、
その稜線上での境界積分は、
以下の面積座標公式によって求めることが出来る。
稜線 ![]() の場合、
の場合、
![]() であるから、
関数
であるから、
関数 ![]() は残りの
は残りの ![]() と
と ![]() を用いて表現され、
を用いて表現され、
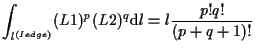 |
(1.29) |
ここで、
![]() は稜線の長さ、
は稜線の長さ、
![]() は0または正の整数である。
は0または正の整数である。
稜線 ![]() の場合、
の場合、
![]() であるから、
関数
であるから、
関数 ![]() は残りの
は残りの ![]() と
と ![]() を用いて表現され、
を用いて表現され、
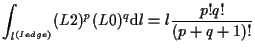 |
(1.30) |
稜線 ![]() の場合、
の場合、
![]() であるから、
関数
であるから、
関数 ![]() は残りの
は残りの ![]() と
と ![]() を用いて表現され、
を用いて表現され、
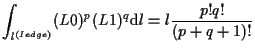 |
(1.31) |
例えば、以下が成り立つ。
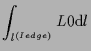 |
|||
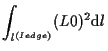 |
|||
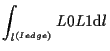 |
|||
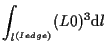 |
|||
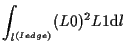 |
(1.32) |