要素 ![]() における
関数
における
関数 ![]() について、
について、
| (5.49) |
その領域積分は、
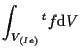 |
|||
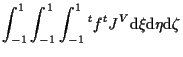 |
|||
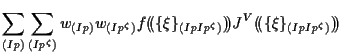 |
ここで、
体積積分の変換子 ![]() は、Jacobianのdeterminantとなり、
は、Jacobianのdeterminantとなり、
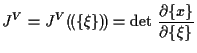 |
(5.50) |
![]() は、
面内および厚み方向の積分点
は、
面内および厚み方向の積分点 ![]() の自然座標であり、
面内方向
の自然座標であり、
面内方向 ![]() には四辺形の積分点
には四辺形の積分点 ![]() の自然座標、
厚み方向
の自然座標、
厚み方向 ![]() は一次元の積分点
は一次元の積分点 ![]() の自然座標を用いる。
の自然座標を用いる。
一般に、
面内方向には四辺形のガウス積分、
厚み方向 ![]() にはニュートンコーツ積分を行う。
にはニュートンコーツ積分を行う。
また、
![]() は、面内方向の四辺形の積分点
は、面内方向の四辺形の積分点 ![]() の重み係数、
の重み係数、
![]() は厚み方向
は厚み方向 ![]() の重み係数である。
の重み係数である。
各方向の数値積分の座標と重みについては、
面内方向には、「数値積分」「ガウス積分」「四辺形」を参照。
![]() 方向には、「数値積分」「ニュートンコーツ積分」を参照。
方向には、「数値積分」「ニュートンコーツ積分」を参照。