要素 ![]() において、
関数
において、
関数 ![]() を
単位面積当りの量を表すものとする。
を
単位面積当りの量を表すものとする。
| (5.51) |
また、この値は自然座標の ![]() にのみ依存する、すなわち、
面内方向にのみ変化するとする。
にのみ依存する、すなわち、
面内方向にのみ変化するとする。
要素の中央面上の積分は、以下のように表される。
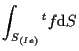 |
|||
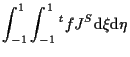 |
|||
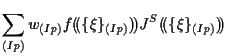 |
ここで、
境界積分の変換子 ![]() は、
は、
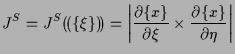 |
(5.52) |
![]() は、
中央面
は、
中央面![]() 上の四辺形の積分点
上の四辺形の積分点 ![]() の自然座標である。
面内方向
の自然座標である。
面内方向 ![]() には四辺形の積分点
には四辺形の積分点 ![]() の自然座標、
厚み方向については、
の自然座標、
厚み方向については、 ![]() となる。
となる。
また、
![]() は、四辺形の積分点
は、四辺形の積分点 ![]() の重み係数である。
の重み係数である。
各方向の数値積分の座標と重みについては、 「数値積分」「ガウス積分」「四辺形」を参照。