要素 ![]() 境界表面
境界表面 ![]() の
要素熱伝達項ベクトル
の
要素熱伝達項ベクトル
![]() は、
表面
は、
表面 ![]() の場合、
の場合、
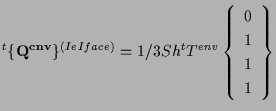 |
(5.35) |
表面 ![]() の場合、
の場合、
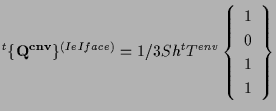 |
(5.36) |
表面 ![]() の場合、
の場合、
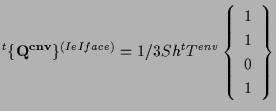 |
(5.37) |
表面 ![]() の場合、
の場合、
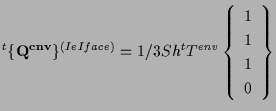 |
(5.38) |
ここで、
![]() は要素
は要素 ![]() 境界
境界 ![]() の面積である。
の面積である。
また、
要素 ![]() 境界表面
境界表面 ![]() の
熱伝達係数
の
熱伝達係数 ![]() と
外部温度
と
外部温度
![]() は、
「熱伝導」「熱伝導境界値問題:線形」
「熱流束境界条件」「熱伝達による熱流束」を参照。
は、
「熱伝導」「熱伝導境界値問題:線形」
「熱流束境界条件」「熱伝達による熱流束」を参照。