解説

時刻$t$において、 物体内の任意の仮想表面上にとった微小な面素 $\mathrm{d} {}^{t} s$ に 作用する力を $\mathrm{d} {}^{t} \{ f^n \}$ とする。 外向単位法線ベクトルを ${}^{t} \{ n \}$ とすると、 応力ベクトル ${}^{t} \{ t \}$ は、 時刻 $t$ の現配置で定義される。

$${}^{t} \{ t \} = \frac{ \mathrm{d} {}^{t} \{ f^n \} }{ \mathrm{d} {}^{t} s } = { {}^{t} [ \sigma ] } ^ { T } \cdot {}^{t} \{ n \}$$ (6.98)

上式はCauchyの公式 Cauchy's formula と呼ばれる。

Cauchyの第１運動法則 Cauchy's first law of motion または平衡方程式 equilibrium equationは、

$${}^{t} \rho {}^{t} \{ a \} = \mathrm{div} {}^{t} [ \sigma ] + {}^... ...b \} = \{ \nabla^{ {}^{t} \{ x \} } \} \cdot {}^{t} [ \sigma ] + {}^{t} \{ b \}$$ (6.99)

あるいは、

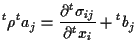$${}^{t} \rho {}^{t} a_j = \frac{ \partial {}^{t} \sigma_{ij} }{ \partial {}^{t} x_i } + {}^{t} b_j$$ (6.100)

Cauchyの第２運動法則 Cauchy's second law of motionより、 Cauchy応力テンソルは対称テンソルである。 したがって、実数の主値（主応力 principal stress）と 主軸（主方向 principal direction）を持つ。

現配置の面素に作用する力を基準配置に平行移動して定義される 応力ベクトル ${}_{o}^{t} \{ \tilde{t} \}$ は、

$${}_{o}^{t} \{ \tilde{t} \} = \frac{ \mathrm{d} {}^{t} \{ f^n \} }{ \mathrm{d} S } = { {}_{o}^{t} [ \Pi ] } ^ { T } \cdot \{ N \}$$ (6.101)

現配置の面素に作用する力に ${ {}_{o}^{t} [ F ] } ^ { -1 }$ をかけて 基準配置の面素に作用させた 応力ベクトル ${}_{o}^{t} \{ \tilde{\tilde{t}} \}$ は、

$${}_{o}^{t} \{ \tilde{\tilde{t}} \} = \frac{ { {}_{o}^{t} [ F ] } ... ... {}^{t} \{ f^n \} } { \mathrm{d} S } = { {}_{o}^{t} [ S ] } ^ { T } \cdot \{N\}$$ (6.102)

したがって、Nansonの公式 6.34 より、

$${}^{t} [ \sigma ] = \frac{1}{ {}_{o}^{t} J } {}_{o}^{t} [ \tau ] ... ... J } {}_{o}^{t} [ F ] \cdot {}_{o}^{t} [ S ] \cdot { {}_{o}^{t} [ F ] } ^ { T }$$ (6.103)

また、以下の関係式が成り立つ。

$${}^{t} [ \sigma ] = {}_{t}^{t} [ \tau ] = {}_{t}^{t} [ \Pi ] = {}_{t}^{t} [ S ]$$ (6.104)