解説

２次元平面歪み問題では、以下が成り立つ。

$${}^{t} \epsilon^e_{zz} = {}^{t} \epsilon^e_{yz} = {}^{t} \epsilon^e_{zx} = 0$$ (8.30)

$${}^{t} \sigma_{yz} = {}^{t} \sigma_{zx} = 0$$ (8.31)

z方向の垂直応力 ${}^{t} \sigma_{zz}$ は０ではなく、 ???????????????????????????????

$${}^{t} \sigma_{zz} = \frac{ \nu E }{ (1 + \nu) (1 - 2 \nu) } ( {}^{t} \epsilon^e_{xx} + {}^{t} \epsilon^e_{yy} )$$

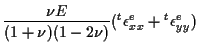$$= \nu ( {}^{t} \sigma_{xx} + {}^{t} \sigma_{yy} )$$ (8.32)

基本的には、３次元ソリッドのものを縮退する。 歪みのzz, yz, zx成分が０であるから、 仮想仕事項の計算には、 弾性定数テンソルのijzz, ijyz, ijzx, ijzy, ijxz成分 およびzzkl, yzkl, zxkl, zykl, xzkl成分を０とする。