要素 ![]() の整合熱容量行列
の整合熱容量行列
![]() の、
節点
の、
節点 ![]() 節点
節点 ![]() における
成分
における
成分
![]() は、
積分範囲
は、
積分範囲 ![]() において、
において、
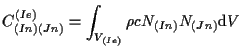 |
(12.26) |
要素 ![]() の質量密度
の質量密度 ![]() 、および、比熱
、および、比熱 ![]() は、
「熱伝導」「熱伝導境界値問題:線形」「熱伝導方程式」を参照。
は、
「熱伝導」「熱伝導境界値問題:線形」「熱伝導方程式」を参照。
各次元/位相、要素タイプにしたがって、 整合熱容量行列の各成分につき、 領域積分を行う。
一方、
集中化(ランプ化)熱容量行列
![]() は、
「偏微分方程式」「未知数スカラーの領域積分項行列」
「集中化行列」を参照。
??????????????????????????????????????????????????
は、
「偏微分方程式」「未知数スカラーの領域積分項行列」
「集中化行列」を参照。
??????????????????????????????????????????????????