材料非線形問題の解法には、一般に増分法が用いられる。
増分法では、
時刻 ![]() の時点で釣り合いが達成されている状態からスタートして、
時刻
の時点で釣り合いが達成されている状態からスタートして、
時刻 ![]() の時点での釣り合い条件を求める。
の時点での釣り合い条件を求める。
時刻 ![]() の時点ではすべての物理量が既知であるとする。
一方、時刻
の時点ではすべての物理量が既知であるとする。
一方、時刻 ![]() の時点では外力のみが既知である。
そこで、時刻
の時点では外力のみが既知である。
そこで、時刻 ![]() での接線剛性を求め、
そこからまず、
未知数である時刻
での接線剛性を求め、
そこからまず、
未知数である時刻 ![]() から 時刻
から 時刻 ![]() への変位増分を求め、
続いて、歪み増分および応力増分を順次求めていくことになる。
への変位増分を求め、
続いて、歪み増分および応力増分を順次求めていくことになる。
この過程は一般的に非線型である。
増分幅 ![]() が大きければ、
接線剛性を時刻
が大きければ、
接線剛性を時刻 ![]() で評価しているので、
一回では釣り合いがとれないことが多い。
そこで、静的/動的陰解法のように、
不釣り合い力に基づいて変位増分を更新し、
不釣り合い力が十分小さくなるまで
この過程を繰り返す手法がとられることが多い。
で評価しているので、
一回では釣り合いがとれないことが多い。
そこで、静的/動的陰解法のように、
不釣り合い力に基づいて変位増分を更新し、
不釣り合い力が十分小さくなるまで
この過程を繰り返す手法がとられることが多い。
あるいは、静的/動的陽解法のように、
増分ステップごとに一度だけ変位増分を求め、
そのかわり、逆に増分幅 ![]() を十分小さくとって、
不釣り合い誤差が無視できるようにする方法もありうる。
を十分小さくとって、
不釣り合い誤差が無視できるようにする方法もありうる。
式
7.12
より、
時刻 ![]() における微小変形問題の仮想仕事の原理式は、
における微小変形問題の仮想仕事の原理式は、
![$\displaystyle \int_V
{}^{t + \Delta t} [ \sigma ] : \delta {}^{t + \Delta t} [ \epsilon ]
\mathrm{d} V
=
\delta {}^{t + \Delta t} R$](img1089.png) |
(7.15) |
さらに、
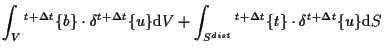 |
|||
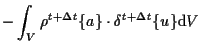 |
(7.16) |
ここで、
![]() は仮想変位、
は仮想変位、
![]() は仮想歪み
である。
は仮想歪み
である。
まず、上式を増分分解する。
変位
![]() を増分分解すると、
を増分分解すると、
| (7.17) |
ここで、
![]() は変位増分である。
は変位増分である。
歪み
![]() を増分分解すると、
を増分分解すると、
| (7.18) |
ここで、
![]() は歪み増分である。
は歪み増分である。
これら変位および歪みの変分をとると、
| (7.19) |
| (7.20) |
また、応力を増分分解すると、
| (7.21) |
ここで、
![]() は応力増分である。
は応力増分である。
以上より、増分型の仮想仕事式は、
さらに、
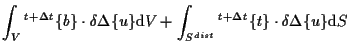 |
|||
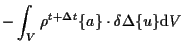 |
(7.23) |
次に、非線型項である最右辺の接線係数を求める。
まず、
![$\displaystyle \lim_{ \Delta t \to 0 } \frac{ \Delta [ \sigma ] }{ \Delta t }
\to {}^{t} [ \dot{\sigma} ]$](img1106.png) |
(7.24) |
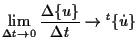 |
(7.25) |
したがって、接線係数は、
![$\displaystyle \lim_{ \Delta t \to 0 } \frac{
\int_V
\Delta [ \sigma ] : \delta \Delta [ \epsilon ]
\mathrm{d} V
}{ \Delta t }$](img1108.png) |
|||
![$\displaystyle \to
\int_V
{}^{t} [ \dot{\sigma} ] : \delta \Delta [ \epsilon ]
\mathrm{d} V$](img1109.png) |
(7.26) |
さらに、 応力増分の式 7.14 より、 これを増分形にして、
なお、ここで用いられている変数としては、
材料定数、
時刻 ![]() でのすべての状態変数および、
荷重
でのすべての状態変数および、
荷重
![]() 、
、
![]()
![]() 、
、
![]() は既知であり、
は既知であり、
![]() 、
、
![]() は未知であり、
一方、
は未知であり、
一方、
![]() は任意の値をとり、
は任意の値をとり、
![]() は
は
![]() より導出される。
より導出される。
また、
時刻 ![]() での
変位
での
変位
![]() 、
応力
、
応力
![]() については、
各増分ステップごとに得られた
変位増分
については、
各増分ステップごとに得られた
変位増分
![]() 、
応力増分
、
応力増分
![]() を用いて更新していく。
を用いて更新していく。