式
7.37
より、
基準時刻 ![]() 、現時刻
、現時刻 ![]() における仮想仕事の原理式は、
における仮想仕事の原理式は、
![$\displaystyle \int_{ {}^{t} v}
{}_{t}^{t + \Delta t} [ S ] : \delta {}_{t}^{t + \Delta t} [ E ]
\mathrm{d} {}^{t} v
=
\delta {}^{t + \Delta t} R$](img1221.png) |
(7.72) |
さらに、
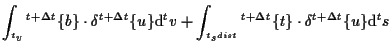 |
|||
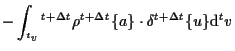 |
(7.73) |
![]() は仮想Green-Lagrange歪みであり、
式
6.48
より、
は仮想Green-Lagrange歪みであり、
式
6.48
より、
| (7.74) |
ここで、
![]() は仮想変位勾配である。
2次元、3次元問題では、それぞれ2次元、3次元テンソル量を用いる。
軸対称問題の場合には、
x, y成分は2次元テンソルで計算し、
zz成分については、
は仮想変位勾配である。
2次元、3次元問題では、それぞれ2次元、3次元テンソル量を用いる。
軸対称問題の場合には、
x, y成分は2次元テンソルで計算し、
zz成分については、
![]() とする。
とする。
まず、上式を増分分解する。
変位
![]() を増分分解すると、
を増分分解すると、
| (7.75) |
ここで、
![]() は変位増分である。
は変位増分である。
Green-Lagrange歪み
![]() を増分分解すると、
を増分分解すると、
| (7.76) |
![]() はGreen-Lagrange歪み増分の線形部分であり、
式
6.48
より、
はGreen-Lagrange歪み増分の線形部分であり、
式
6.48
より、
| (7.77) |
ここで、
![]() は変位勾配増分である。
2次元、3次元問題では、それぞれ2次元、3次元テンソル量を用いる。
軸対称問題の場合には、
x, y成分は2次元テンソルで計算し、
zz成分については、
は変位勾配増分である。
2次元、3次元問題では、それぞれ2次元、3次元テンソル量を用いる。
軸対称問題の場合には、
x, y成分は2次元テンソルで計算し、
zz成分については、
![]() とする。
とする。
![]() はGreen-Lagrange歪み増分の非線形部分であり、
式
6.48
より、
はGreen-Lagrange歪み増分の非線形部分であり、
式
6.48
より、
| (7.78) |
これら変位および歪みの変分をとると、
| (7.79) |
| (7.80) |
| (7.81) |
| (7.82) |
ここで、
![]() は仮想変位勾配増分である。
は仮想変位勾配増分である。
![]() については、
2次元、3次元問題では、それぞれ2次元、3次元テンソル量を用い、
軸対称問題の場合には、
x, y成分は2次元テンソルで計算し、
zz成分については、
については、
2次元、3次元問題では、それぞれ2次元、3次元テンソル量を用い、
軸対称問題の場合には、
x, y成分は2次元テンソルで計算し、
zz成分については、
![]() とする。
とする。
また、第2Piola-Kirchhoff応力を増分分解すると、
| (7.83) |
ここで、
![]() はCauchy応力、
はCauchy応力、
![]() は第2Piola-Kirchhoff応力増分である。
は第2Piola-Kirchhoff応力増分である。
以上より、増分型の仮想仕事式は、
さらに、
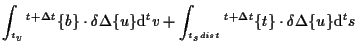 |
|||
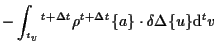 |
(7.85) |
次に、非線型項である最右辺の接線係数を求める。
まず、
![$\displaystyle \lim_{ \Delta t \to 0 } \frac{ \Delta {}_{t} [ S ] }{ \Delta t }
\to {}_{t}^{t} [ \dot{S} ]$](img1251.png) |
(7.86) |
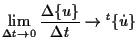 |
(7.87) |
![$\displaystyle \lim_{ \Delta t \to 0 } \frac{ \Delta {}_{t} [ Z ] }{ \Delta t }
\to {}_{t}^{t} [ \dot{Z} ]$](img1252.png) |
(7.88) |
したがって、接線係数は、
![$\displaystyle \lim_{ \Delta t \to 0 } \frac{
\int_{ {}^{t} v}
\Delta {}_{t} [ S...
... [ \sigma ] : \delta \Delta {}_{t} [ E^{NL} ]
\mathrm{d} {}^{t} v
}{ \Delta t }$](img1253.png) |
|||
![$\displaystyle \to \int_{ {}^{t} v}
{}_{t}^{t} [ \dot{S} ] : \delta \Delta {}_{t...
...t} [ \sigma ] : ( \delta \Delta {}_{t} [ E^{NL} ] )^{\cdot}
\mathrm{d} {}^{t} v$](img1254.png) |
(7.89) |
ここで、
| (7.90) |
もし、構成式に相対Kirchhoff応力のJaumann速度を用いる場合、 応力増分の式 7.61 より、 これを増分形にして、
このとき、接線剛性行列は対称となる。
もし、構成式にCauchy応力のJaumann速度を用いる場合、 応力増分の式 7.62 より、
このとき、接線剛性行列は非対称となる。
なお、ここで用いられている変数としては、
材料定数、
時刻 ![]() でのすべての状態変数および、
荷重
でのすべての状態変数および、
荷重
![]() 、
、
![]() は既知であり、
は既知であり、
![]() 、
、
![]() は未知であり、
一方、
は未知であり、
一方、
![]() は任意の値をとり、
は任意の値をとり、
![]() は
は
![]() より導出される。
より導出される。
また、
時刻 ![]() での
変位
での
変位
![]() 、
応力
、
応力
![]() については、
各増分ステップごとに得られた
変位増分
については、
各増分ステップごとに得られた
変位増分
![]() 、
応力増分
、
応力増分
![]() を用いてそれぞれ更新していく。
このとき、応力増分の計算には
Cauchy応力増分の式
7.63
を用いる。
を用いてそれぞれ更新していく。
このとき、応力増分の計算には
Cauchy応力増分の式
7.63
を用いる。