![$\displaystyle \int_V
[[ C ]] : {}^{t} [ \epsilon ] : \delta {}^{t} [ \epsilon ]
\mathrm{d} V$](img1076.png) |
|||
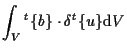 |
|||
![$\displaystyle +
\int_V
[[ C ]] : {}^{t} [ \epsilon^o ] : \delta {}^{t} [ \epsil...
...hrm{d} V
-
\int_V
{}^{t} [ \sigma^o ] : \delta {}^{t} [ \epsilon ]
\mathrm{d} V$](img1077.png) |
|||
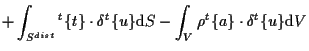 |
(11.28) |
微小変形線形弾性での仮想仕事の原理式は、 (式 7.12 参照)
![$\displaystyle \int_V
[[ C ]] : {}^{t} [ \epsilon ] : \delta {}^{t} [ \epsilon ]
\mathrm{d} V$](img1076.png) |
|||
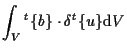 |
|||
![$\displaystyle +
\int_V
[[ C ]] : {}^{t} [ \epsilon^o ] : \delta {}^{t} [ \epsil...
...hrm{d} V
-
\int_V
{}^{t} [ \sigma^o ] : \delta {}^{t} [ \epsilon ]
\mathrm{d} V$](img1077.png) |
|||
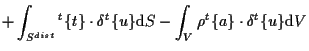 |
(11.28) |
ここで、 左辺は仮想仕事量(歪みエネルギー)、 右辺第1項は体積力仕事、 右辺第2項は初期歪みによる見掛けの仕事、 右辺第3項は初期応力による見掛けの仕事、 右辺第4項は表面力仕事(分布荷重、圧力荷重、および集中荷重による仕事)、 右辺第5項は加速度による慣性力の仕事 である。
これに上記の未知数の有限要素補間式を代入すると、 (各項については、以下の各節で具体例に説明する。)
| (11.29) |
ここで、
要素 ![]() について、
について、
![]() は
要素剛性行列
は
要素剛性行列
![]() の
節点
の
節点 ![]() 自由度
自由度 ![]() 節点
節点 ![]() 自由度
自由度 ![]() に関する成分である。
に関する成分である。
![]() は
要素減衰行列
は
要素減衰行列
![]() の
節点
の
節点 ![]() 自由度
自由度 ![]() 節点
節点 ![]() 自由度
自由度 ![]() に関する成分である。
に関する成分である。
![]() は
要素質量行列
は
要素質量行列
![]() の
節点
の
節点 ![]() 自由度
自由度 ![]() 節点
節点 ![]() 自由度
自由度 ![]() に関する成分である。
に関する成分である。
![]() は
要素体積力項ベクトル
は
要素体積力項ベクトル
![]() の
節点
の
節点 ![]() 自由度
自由度 ![]() に関する成分である。
に関する成分である。
![]() は
要素初期歪み項ベクトル
は
要素初期歪み項ベクトル
![]() の
節点
の
節点 ![]() 自由度
自由度 ![]() に関する成分である。
に関する成分である。
![]() は
要素初期応力項ベクトル
は
要素初期応力項ベクトル
![]() の
節点
の
節点 ![]() 自由度
自由度 ![]() に関する成分である。
に関する成分である。
要素 ![]() の境界
の境界 ![]() について、
について、
![]() は
要素分布荷重項ベクトル
は
要素分布荷重項ベクトル
![]() の
節点
の
節点 ![]() 自由度
自由度 ![]() に関する成分である。
に関する成分である。
![]() は
要素圧力荷重項ベクトル
は
要素圧力荷重項ベクトル
![]() の
節点
の
節点 ![]() 自由度
自由度 ![]() に関する成分である。
に関する成分である。
節点 ![]() について、
について、
![]() は
全体集中荷重項ベクトル
は
全体集中荷重項ベクトル
![]() の
節点
の
節点 ![]() 自由度
自由度 ![]() に関する成分である。
に関する成分である。
この式は、任意の仮想変位自由度
![]() について
成り立たねばならないから、すべての自由度
について
成り立たねばならないから、すべての自由度 ![]() について、
について、
| (11.30) |
すなわち、
| (11.31) |
ここで、
![]() 、
、
![]() 、
、
![]() はそれぞれ、
システム全体での変位、速度、加速度の列ベクトルである。
はそれぞれ、
システム全体での変位、速度、加速度の列ベクトルである。
そして、最終的に上記の有限要素離散化式が得られる。