ガウス積分

ガウス積分では、 多項式関数の数値積分結果が厳密積分と一致した上で、 その積分区間上の積分点数が最小となるように、 積分点の位置およびそれぞれの重み係数を選択する。

まず、 一次元の線分区間 $-1 \le \xi \le 1$ における 多項式 $f$ のガウス積分は以下のようになる。

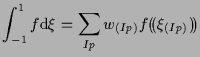$$\int_{-1}^1 f \mathrm{d} \xi = \sum_{Ip} w_{(Ip)} f ( \! ( \xi_{(Ip)} ) \! )$$ (3.1)

このとき、 必要な積分点 $Ip$ の総数および、 各積分点の位置 $\xi_{(Ip)}$ と重み係数 $w_{(Ip)}$ は、 積分される多項式 $f$ の次数により決定される。

また、これを用いて、 二次元長方形領域 $-1 \le \xi \le 1$ 、 $-1 \le \eta \le 1$ や、 三次元直方体領域 $-1 \le \xi \le 1$ 、 $-1 \le \eta \le 1$ 、 $-1 \le \zeta \le 1$ へ 適用することができる。

さらに、二次元の三角形領域、三次元の四面体領域については、 それら向けに特別に選択された積分点のセットが存在する。